Расчет тяговых характеристик автомобиля |
Реферат
С.
20, рис. 1, табл. 1., формул 36, приложений 1.
Ключевые
слова: тяговый расчёт, автомобиль, прототип, Mitsubishi Galant, двигатель, трансмиссия, внешняя скоростная
характеристика, динамический фактор, тяговый баланс, мощностной баланс.
В
этой работе проводится тяговый расчёт проектируемого автомобиля.
В
первой части выбран автомобиль-прототип Mitsubishi Galant, а также дана его краткая техническая характеристика.
Во
второй части проведены расчёты основных параметров двигателя – мощности и
крутящего момента.
В
третьей части работы проведены расчёты трансмиссии, в результате которых
получены передаточные отношения ступеней по гиперболическому ряду, а также
передаточное отношение главной передачи.
В
четвёртой части работы проведена оценка полученных параметров двигателя и
трансмиссии методами тягового баланса, мощностного баланса, а также оценка по
динамическому фактору.
В
заключение представлен анализ полученных результатов на основе оценки
параметров по трём методам.
Графики
полученных результатов, а также сводные таблицы результатов вынесены в
приложение 1.
В результате работы
были достигнуты положительные результаты – рассчитанные параметры двигателя и
трансмиссии удовлетворяют техническому заданию, и позволяют достичь необходимых
параметров производительности.
Ориентировочно полная масса легкового автомобиля может быть определена по формуле [1, стр. 6, ф. (1.1)]:
𝑚𝑎 = 𝑚0 + 75𝑛пас + 𝑚гр, (1)
где 𝑚𝑎 – масса снаряженного автомобиля, кг (принимаем равным 1300 кг), кг; 75 – масса одного пассажира, кг; nпас – число пассажиров, включая водителя (принимаемым равным показателю автомобиля-прототипа); mгр – масса багажа (принимаем равным 30 кг).
𝑚𝑎 = 1300+ 75 ∙ 5 + 30 =
1705 кг
Шины рассчитываемого автомобиля примем 215/60R16.
Коэффициент
полезного действия трансмиссии принимаем равным 0,92 согласно справочным данным
для легковых автомобилей [1, стр. 6]. тр
Коэффициент
обтекаемости назначается равным kв=0,4 Н∙ с2/м4 в
соответствии с результатами исследований, приведённых в [1, с.7, табл.1].
Площадь лобового сечения автомобиля определяется с помощью формулы [1, стр. 7, ф.1.4]:
𝐹𝑎 = 𝑎𝐵𝐻, (1)
где 𝐵 – ширина машины, м; 𝐻 – высота автомобиля, м; a – коэффициент заполнения площади (a = 0,78–0,8 – для легковых автомобилей; назначено a=0,8)
𝐹𝑎 = 0.8 ∙ 1.740 ∙ 1.415 ≈ 1.96 м2
1.2 Выбор
характеристики двигателя
Необходимая максимальная мощность двигателя Nev предварительно определяется по формуле [1, стр. 7, ф. 1.5]:
𝑁𝑒𝑣 = 1/ 𝜂тр (9,8𝑚𝑎𝜓𝑣 *𝑣𝑚𝑎𝑥 /3.6 + 𝑘𝑒𝐹𝑎* 𝑣𝑚𝑎𝑥 3 /46,656) 10−3, (2)
где – коэффициент сопротивления дороги; – максимальная скорость движения автомобиля км/ч. v max v
Коэффициент сопротивления дороги определяется по эмпирической формуле:
𝜓𝑣 = 𝑓𝑣 = 0.02 (1 + 𝑣𝑚𝑎𝑥 2 /1500) = 0.02 (1 + 55.55^2/1500) = 0.043, (3)
где – максимальная скорость автомобиля в м/с. max v
Таким образом,
подставляя результат вычислений по формуле (4) в формулу (3) получим
необходимую максимальную мощность Nev:
𝑁𝑒𝑣 = 1 /0,92 (9,8 * 1705 * 0,043 ∙ 200 /3.6 + 0,4 ∙ 1.96 ∙ 200^3 /46,656) ∙ 10−3 = 206.6602105
Максимальная мощность бензинового двигателя выражается из формулы С. Р. Лейдермана [1, стр. 8, ф. 1.7]:
𝑁𝑚𝑎𝑥 = 𝑁𝑒𝑣 (𝑛𝑚𝑎𝑥 /𝑛𝑁 ) + (𝑛𝑚𝑎𝑥/ 𝑛𝑁 )2 − (𝑛𝑚𝑎𝑥 𝑛𝑁 )3 , (5)
где nN – номинальная частота вращения вала, об/мин (принята аналогично автомобилю- прототипу 5000 об/мин).
Максимальная частота вращения коленчатого вала nmax определяется по формуле [1, стр. 8]:
𝑛𝑚𝑎𝑥 = 1,15𝑛𝑁 = 1,15 ∙ 6000 = 6900 об мин , (6)
По формуле (5) производится расчёт максимальной мощности
бензинового двигателя:
𝑁𝑚𝑎𝑥 = 208 (6900 /6000) + (6900/ 6000)2 − (6900/6000)3
= 239.0016 кВт
График зависимости вала N e = f(n) вычисляется с помощью уравнения С. Р. Лейдермана [1, стр. 9, ф. 1.8]:
𝑁𝑒𝑖 = 𝑁𝑚𝑎𝑥 [𝑎 (𝑛𝑖/ 𝑛𝑁) + 𝑏 ( 𝑛𝑖/ 𝑛𝑁)^2 − 𝑐 ( 𝑛𝑖/ 𝑛𝑁)^3] , (7)
где a, b, c – эмпирические коэффициенты зависящие от типа двигателя (для бензинового двигателя ); ni – текущее значение частоты вращения коленчатого вала, об/мин.
Минимальная частота вращения коленчатого вала nmin принята равной 800 об/мин согласно справочным данным [1, стр. 9].
Пример расчёта крутящего момента при 800 об/мин:
𝑁𝑒𝑖 = 239.0016* [( 800/ 6000) + ( 800/6000)2 − ( 800/ 6000)3] = 31.883 кВт
Результаты расчетов при остальных оборотах двигателя сведены в табл. П.. 1 приложения 1.
График зависимости крутящего момента от частоты вращения коленчатого вала строится с использованием зависимости [1, стр. 9, ф. 1.9]:
Mei = 9.554*10^3*(Nei/ni);
Пример расчёта крутящего момента при 800 об/мин:
Mei = 366.7138 Н·м.
Результаты
расчетов при остальных оборотах двигателя сведены в табл. П.1 приложения 1.
График внешней скоростной характеристики двигателя
представлен в приложении 1 (рис. П1).
1.3 Выбор параметров
трансмиссии
Передаточное число главной передачи коробки передач из
условия обеспечения максимальной кинематической скорости автомобиля [1, стр.
10, ф. 1.10]:
где iвп –
передаточное число высшей передачи коробки передач; vmax –
максимальная скорость по заданию, км/ч; rк – радиус
качения колеса, м.
Радиус качения колес rк определяется по формуле [1, стр. 10, ф. 1.11]:
где d0 – диаметр обода колеса; Bш – ширина профиля шины; ш – коэффициент деформации
(принят 0,87 [1, стр. 11]).
Согласно выбранному обозначению
шины 215/60R16 97Q,
вышеуказанные величины будут
равны: d0 = 306,8 мм (для 16 дюймов); Bш = 215мм; ш = 0,87
(согласно рекомендациям [1, c.11, табл.4]). После подстановки назначенных величин в формулу
(10), было получено следующее значение радиуса качения колеса rк.
rк= 0.3693
Подставляя в формулу (5) результата вычисления по формуле (6), получим:
i0 = 4.8033
Определение передаточного числа первой передачи исходя из условий:
1. Возможность
преодоления автомобилем заданного максимального дорожного сопротивления [1,
стр. 12, ф. 1.12]:
i1= 2.5796
где – коэффициент
суммарного дорожного сопротивления (принят 0,5); – максимальный крутящий момент
двигателя (достигается на 2400 об/мин).
2. Возможности полной
реализации сцепной массы автомобиля [1, стр. 12, ф. 1.13]:
i1= 3.8694
где – коэффициент
сцепного веса автомобиля (для полноприводного автомобиля принят 1); –
коэффициент сцепления шин с дорогой (для сухой дороги с асфальтовым покрытием
принят 0,75). сц k
3. Обеспечение
минимальной устойчивой скорости движения в заданных дорожных условиях [1, стр.
12, ф. 1.14]: min v
i1= 4.67377
где min v – принята 5 км/ч для автомобиля нормальной проходимости.
Т. к. передаточное отношение
первой передачи i1 больше по третьему условию – то оно
принимается в качестве
расчётного, т. о. 4,173 1 i .
Передаточное отношение
промежуточных, 2, 3 и 5 ступеней КПП рассчитано по
гиперболическому ряду, как
обеспечивающего лучшую динамику автомобиля на высоких
скоростях [2, стр. 18]:
где k – номер
рассчитываемой передачи; n – номер прямой передачи (принят 4-й, потому что её
передаточное число равно 1).
По формуле (10) рассчитаны передаточные отношения 2, 3 и
5 передачи:
для k = 2
i2=
2.0961
для k = 3
i3=
1.3540
для k = 5
i5= 0.7927
1.4 Оценка
тягово-скоростных свойств автомобиля
Для проверки правильности выбора параметров двигателя и
трансмиссии применим метод силового баланса. Уравнение силового баланса имеет
вид [1, стр. 14, ф. 1.16]:
P T = P f+ P h+ P w+ P j
где P T– сила тяги развиваемая автомобилем; P f – сила сопротивления качению; P h – сила
сопротивления подъёму; P w – сила сопротивления воздуха; P j– сила сопротивления разгону.
Сила тяги P T (Н) рассчитана по формуле [1, стр. 14, ф. 1.17]:
где iКПП –
передаточное число соответствующей ступени коробки передач.
Пример расчета силы тяги PT при n 800 об/мин на первой передаче:
PT= 21294H
Результаты расчёта силы тяги P T при различных оборотах на каждой из 5-ти передач
представлены в приложении: табл.
П.2, табл. П.3, табл. П.4, табл. П.5, табл. П.6.
Скорость
движения автомобиля рассчитывается по формуле [1, стр. 14, ф. 1.18]:
Пример расчёта скорости движения автомобиля при n= 800 об/мин на
первой передаче:
Vi= 4.9614 км/ч
Результаты расчёта скорости движения автомобиля при различных оборотах на
каждой из 5-ти передач представлены в приложении: табл. П.2, табл. П.3, табл.
П.4, табл. П.5, табл. П.6.
По результатам расчётов силы тяги
P T и скорости движения автомобиля на различных
оборотах на каждой из 5-ти
передач, построен график зависимости P T f (v) представленный
вприложении на рис. П.2.
Расчет суммарных сил
сопротивления движению автомобиля для случая равномерного движения автомобиля
по горизонтальной дороге с асфальтовым покрытием (т. е. сила сопротивления
разгону P j 0, сила сопротивления подъёму P h 0, ), производится по формуле [1,
стр. 16, ф. 1.23]:
Сила сопротивления качению P f определяется по формуле [1, стр. 16, ф. 1.19]:
где – угол подъёма дороги при движении автомобиля на подъёме; f v – коэффициент,
зависящий от скорости движения, определяется по формуле 3), вместо max v подставляется
текущее значение скорости автомобиля в м/с.
Пример расчёта силы сопротивления качению P f на высшей передаче при
n 800 об/мин:
P f = 9.8* 1705* 0. 020.Cos0 ~ 334H
Результаты расчёта силы сопротивления качению P f на высшей передаче при различных
оборотах представлены в приложении табл. П.7.
Сила сопротивления воздуха w P определяется по формуле [1, стр. 16, ф. 1.22]:
где Vi– скорость движения автомобиля подставляется м/с.
Пример расчёта силы сопротивления воздуха Pw на высшей передаче при n= 800 об/мин:
Pw= 20H
Результаты расчёта силы
сопротивления воздуха P w на высшей передаче при различных
оборотах представлены в
приложении табл. П.7.
Пример расчёта суммарной силы
сопротивления P Σ на высшей передаче при
n = 700об/мин:
P Σ = 334 + 20= 354H
Результаты расчёта суммарной силы
сопротивления P Σ на высшей передаче при
различных оборотах представлены в
приложении табл. П.7. Кривая суммарной силы
сопротивления представлена в
приложении рис. П.2.
Проверка достижимости
максимальной скорости автомобилем проводится с помощью
уравнения силового баланса (11), при максимальных оборотах двигателя ( n =5770об/мин):
=2440 H
Уравнение баланса выполняется, следовательно, максимальная скорость,
заданная по техническому заданию 200 км/ч достигается при данных параметрах
двигателя и трансмиссии.
Это также видно при анализе
графика рис. П.2. – кривая силы тяги PT на 4-й передаче сходится с
кривой суммарного сопротивления
движению автомобиля P (рассчитанной
на той же 4-й
передаче), проведя проекцию
которой на ось абсцисс, получается 200 км/ч.
Проведём проверку соответствия
рассчитанных параметров двигателя и трансмиссии
методом мощностного баланса. Уравнение мощностного баланса имеет вид[1,
стр. 16, ф. 1.24]:
где NT –
мощность, подводимая к ведущим колесам автомобиля; Nf –
мощность, необходимая для преодоления силы сопротивления подъему; Nw –
мощность, необходимая для преодоления силы сопротивления воздуха; Nj –
мощность, необходимая для разгона автомобиля.
Мощность передаваемая на ведущие колёса автомобиля NT определяется
по формуле [1, стр. 16, ф. 1.25]:
где i v – скорость движения автомобиля подставляется м/с.
Пример расчёта мощности
подводимой к колёсам автомобиля NT при n 800 об/мин на
первой передаче:
NT = 10.559кВт.
Результаты расчёта мощности
подводимой к колёсам автомобиля NT при различных
оборотах на каждой из 5-ти
передач представлены в приложении: табл. П.2, табл. П.3, табл. П.4,
табл. П.5, табл. П.6.
По результатам расчётов мощности
подводимой к колёсам автомобиля NT на различных
оборотах на каждой из 5-ти
передач, построен график зависимости N T f (v) представленный в
приложении на рис. П.3.
Расчет мощности для преодоления
суммарных сил сопротивления движению P
автомобиля для случая
равномерного движения автомобиля по горизонтальной дороге с
асфальтовым покрытием (т. е. сила
сопротивления разгону P j 0, следовательно и N j 0, сила
сопротивления подъёму P h 0, следовательно и N h 0), производится по формуле[1, стр. 18, ф. 1.29]:
Мощность необходимая для преодоления силы сопротивлению качению Nf определяется по формуле [1, стр. 16, ф. 1.26]:
i – скорость движения автомобиля подставляется м/с.
Пример расчёта мощности подводимой к колёсам автомобиля Nf на высшей передаче:
Nf = 1.662 кВт.
Результаты расчёта силы
сопротивления воздуха w P на высшей передаче при различных
оборотах представлены в
приложении табл. П.7.
Мощность необходимая для
преодоления силы сопротивления воздуха Nw определяется
по формуле [1, стр. 16, ф. 1.28]:
где v i – скорость движения автомобиля подставляется м/с, ответ в
Вт.
Пример расчёта мощности
необходимой для преодоления силы сопротивления воздуха
Nw на высшей передаче:
Nw = 95.74 = 0.095
Результаты расчёта мощности
необходимой для преодоления силы сопротивления
воздуха Nw на высшей передаче при различных оборотах представлены в
приложении табл. П.7.
Пример расчёта мощности
необходимой для преодоления суммарной силы
сопротивления на высшей передаче при n 800 об/мин:
N = 1.622+0.095=1.717
Результаты расчёта мощности
необходимой для преодоления суммарной силы
сопротивления P на высшей передаче при различных оборотах представлены в
приложении
табл. П.7. Кривая мощности
необходимой для преодоления суммарной силы сопротивления
представлена в приложении рис.
П.3.
Проверка достижимости
максимальной скорости автомобилем проводится с помощью
уравнения мощностного баланса (18), при максимальных оборотах двигателя
( n 5570об/мин):
=135.42 кВт.
Уравнение баланса выполняется,
следовательно, максимальная скорость, заданная по
техническому заданию 200 км/ч
достигается при данных параметрах двигателя и трансмиссии.
Это также видно при анализе
графика рис. П.3. – кривая силы тяги NT на 4-й передаче сходится с
кривой мощности необходимой для
преодоления суммарного сопротивления движению
автомобиля P (рассчитанной на той же 4-й передаче), проведя проекцию
которой на ось абсцисс,
получается 200 км/ч.
Для получения динамической
характеристики рассчитаем динамический фактор D a по
формуле [1, стр. 18, ф. 1.30]:
где – вес автомобиля, Н, который вычисляется по формуле: Ga
Пример расчёта динамического фактора D a при n 800 об/мин на первой передаче:
Ga = 1705* 9.8 = 16709H
D a = 1.27
Результаты расчёта динамического
фактора D a при различных
оборотах на каждой из 5-
ти передач представлены в
приложении: табл. П.2, табл. П.3, табл. П.4, табл. П.5, табл. П.6.
По результатам расчётов
динамического фактора и скорости движения автомобиля на
различных оборотах на каждой из
5-ти передач, построен график зависимости D a = f (v)
Коэффициент масштаба для
построения номограммы динамического фактора D a ,
вычисляется по формуле [1, стр. 18, ф. 1.31]:


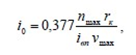




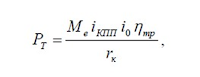











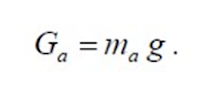
Comments